1 Projet I22 - Python avancé 2013-2014 - J. Razik, C. Nguyen (I22 SABDFL)
Table des matières
L'objectif principal de ce module et de ce projet est de vous familiariser et de respecter les bonnes pratiques de programmation. En effet, la réalisation d'un projet fonctionnel qui brille n'est pas l'objectif premier, ce qui est important est la réalisation d'un code propre.
L'écriture d'un tel code est certes plus longue au début mais apporte un gain de temps énorme au fur et à mesure de la progression du projet. Il est à proscrire ce que l'on appelle les codes ”spaghettis”.
Pour cela vous devez donc mettre en pratique les connaissances acquises durant vos différents module de programmation en Python et d'algorithmique mais également des notions essentielles au développement d'applications telles que la modularité, la protection, la générécité, réutilisabilité, robustesse, évolutivité. Pour cela vous devrez respecter au maximum les PEP8 et PEP257 sur les conventions d'écriture du code et sur l'utilisation de documentation (commentaires). Vous devez également mettre en place pour vos fonctions des tests unitaires validant le bon fonctionnement des dites fonctions.
L'évaluation se fera sur la base du respect du cahier des charges, de la qualité de la programmation (comprenant le style de code et la présence de commentaires pertinents, documentation, tests), des objectifs atteints et des options réalisées.
1.1 Présentation du sujet
Le projet à réaliser est une simulation de combat aérien durant la 1ère Guerre Mondiale. Dans ce jeu pour deux joueurs en ”hot seat”, chaque joueur dirige un avion et tentera d'abattre l'avion adverse. Pour ce faire, chacun dispose d'un avion qui va se déplacer sur l'espace de jeu et d'un ensemble de manœuvres pour programmer les déplacements.
Chaque avion est représenté en vue du dessus et dispose d'un ensemble de manœuvres qui lui est propre (glissade à droite ou à gauche, décrochage, piqué, etc.). Certains avions sont plus robustes mais plus lents, d'autres plus manœuvrables mais plus fragiles. Chaque avion possède donc une vitesse, des points de structure et une portée de tir qui le caractérisent.
Chaque joueur contrôlant un avion planifie son tour de jeu en choisissant une séquence de trois manœuvres. Ensuite l'application simule la première manœuvre de chaque avion en même temps, puis la deuxième et enfin la troisième. Les mouvements sont donc exécutés simultanément (remarque : les avions peuvent se chevaucher). Un avion en dehors de l'aire de jeu à la fin d'un tour (de trois manœuvres) est éliminé. Le joueur avec son avion sur l'aire de jeu, après l'élimination ou la sortie de l'avion adverse, a gagné la partie.
Si un avion peut faire feu durant ses manœuvres, il le fait automatiquement. Le résultat de chaque tir est déterminé aléatoirement et peut occasionner des dégâts. Les dégâts se soustraient aux points de structure d'un avion et sont cumulatifs. Si un avion n'a plus de points de structure il perd la partie.
Vous trouverez des ressources utiles à la réalisation de ce projet (images d'avions, de terrains) dans le fichier avions.tar .
1.2 Cahier des charges
L'environnement est défini par un fond représentant la vue aérienne d'une région et par les avions qui évoluent au dessus.
Les avions doivent être caractérisés par exemple par:
- Un ensemble de manœuvres (vitesse),
- Des points de structure (entre 10 et 20 points),
- Distance de tir.
D'autres caractéristiques peuvent être envisagées (type de dégâts). Toutes les manœuvres se font dans le même plan, il n'y a pas de notion d'altitude.
Pour des raisons à la fois pratique et pour maintenir un certain équilibre les trajectoires doivent s'inscrire dans un rectangle maximal englobant de dimension unique. C'est-à-dire que chaque trajectoire n'utilisera pas forcément la totalité du rectangle englobant mais toutes resteront dedans. Par exemple un avion allant en ligne droite à la vitesse moitié de la vitesse maximale ne parcourra que la moitié du rectangle englobant.
Les tirs sont automatiques et ont lieu une seule fois par manœuvre dès que les conditions de portée et d'angle de tir sont réunis. Ils peuvent entraîner l'enrayage de la mitrailleuse suivant une probabilité de 0,1. Les dégâts sur un avion ennemi se soustraient aux points de structure de l'avion. Ils sont déterminés aléatoirement sur un intervalle de 1 à 5 points.
Le programme prendra en paramètre le nom des avions de chacun des deux adversaires. Une fois l'interface lancée, celle-ci doit permettre:
- à deux joueurs partageant la même machine de programmer trois manœuvres consécutives pour leur avion, (utilisation de deux partie séparées du clavier pour chaque joueur)
- de visualiser le résultat de ces manœuvres (animation des avions sur la carte),
- de prendre en compte les dégâts,
- de gérer les tours (et donc la fin d'un tour),
- de déterminer le vainqueur.
1.3 Aspect technique
Dans l'archive indiquée en début de sujet se trouve les images (sprites) au format png correspondants aux 4 types d'avions suivant:
- albatros,
- fokker,
- sopwith,
- spad.
La taille originale de ces images est 80×80 pixels.
Ce sont également les noms des avions à indiquer en paramètre de la ligne de commande de votre programme. Par exemple pour une démarrer une partie avec un avion de type albatros et un avion de type fokker, la commande à exécuter ressemblera nom_de_votre_programme albatros fokker
L'image de fond représentant le champs de bataille est le fichier photo_aerienne.jpg, image sur laquelle seront dessinés les avions. La taille originale de cette image est de 5557×3745 pixels.
Dans le cadre d'une programmation impérative structurée, il est fortement recommandé d'utiliser des dictionnaires comme structures de données quand cela est possible.
Les manœuvres s'inscrivent dans une trajectoire plane définie par un système paramétrique et un domaine de définition. L'exemple le plus simple est la manœuvre en ligne droite caractérisée par le système paramétrique x = 0, y = t avec t parcourant l'intervalle de 0 à max suivant un certain pas. Les virages larges peuvent être assimilés à des arcs d'ellipses, les virages courts à des arcs de cercles et les glissades à des hystérésis.
Exemples :
Les manœuvres ayant lieu simultanément, il est impératif que toutes les courbes comportent le même nombre de pas de discrétisation, ceci afin de synchroniser naturellement les mouvements des deux avions.
Pour les trajectoires courbes (la glissade est un cas à part) il est nécessaire de calculer à chaque pas l'orientation de l'avion, ce que l'on peut faire aisément pas le calcul de la dérivée en chaque point qui nous donne naturellement la pente de la tangente en ce point.
Pour effectuer les transformations idoines aux sprites des avions, vous utiliserez le module cng. Cette bibliothèque permet de manipuler de nombreux formats d'images (PNG en particulier) et d'effectuer des transformations géométriques sur celles-ci (notamment rotation et dilatation). Néanmoins il est tout de même nécessaire de formaliser un certain nombre de points aussi bien techniques que mathématiques.
Le chargement d'une image se fait par l'appel à la méthode image() avec le nom du fichier, et renvoie un tuple descripteur de l'image qui pourra être manipulé (affiché, modifié).
Pour afficher une image, vous utiliserez la méthode image_draw(px, px, pim) qui permet d'afficher dans la fenêtre l'image pim aux coordonnées (px, py).
La rotation d'angle α (en degrés) s'effectue avec la méthode image_rotate() et la dilatation d'une image avec image_scale(). Pour plus de détails sur les paramètres et les méthodes définies dans le module cng, n'hésitez pas à utiliser la commande help(cng) dans l'interpréteur python.
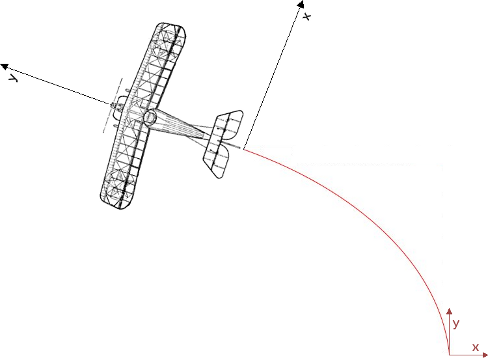
Dans le contexte d'une modification de l'image originale du sprite en fonction de la trajectoire suivie, il est conseillé de faire coïncider origine et direction de l'image et de la courbe. C'est pourquoi le domaine de définition du paramètre t doit correspondre à une portion de courbe débutant à l'origine et ayant une direction générale verticale (comme dans les exemples ci-dessus). Dans ces conditions, il reste à effectuer un changement de repère pour tenir compte de la manœuvre précédente. On rappelle les équations paramétriques de la rotation vectorielle :
x' = x*cos(alpha) - y*sin(alpha)
y' = x*sin(alpha) + y*cos(alpha)
Ainsi que les propriétés du produit scalaire (qui permet de calculer le cosinus de l'angle entre deux vecteurs, directement si les deux vecteurs sont unitaires) et du produit vectoriel (qui permet de savoir dans quel sens on tourne : sens direct ou indirect).
Par exemple, sur le schéma de la figure précédente, l'avion a pour position (-300, 300) dans le repère initial (en rouge) et bien entendu (0, 0) dans le nouveau repère associé à la prochaine manœuvre (en noir). De même, son orientation est déterminée par le vecteur (-1/2, 4/5) dans le repère initial et par le vecteur (0, 1) dans le nouveau repère.
Pour résoudre simplement le problème de la portée et de l'arc de tir, il suffit de procéder en deux étapes : déterminer si la cible est à portée en comparant la distance qui sépare l'avion de sa cible et la portée de l'arme. Pour cela, on peut utiliser le cercle englobant les avions et tester les distances par rapport aux rayons des-dits cercles et de la portée. Puis, si c'est le cas, utiliser une fois encore le produit scalaire pour établir si la cible est dans l'angle de tir.
1.4 Interface
L'interface du jeu pourra se présenter ainsi :
- La partie principale de la fenêtre sera consacrée `a la représentation du terrain d'évolution des avions et du combat,
- La partie inférieure de la fenêtre sera consacrée aux informations
sur le déroulement de la partie :
- Nombres de manoeuvres entrées/disponibles (figures 3a et 3b),
- Déroulement des manoeuvres pendant la phase de simulation (figure 3c}).
Figure 3a, 3b et 3c
Figure 4
Le projet devra obligatoirement prendre en compte les 5 trajectoires suivantes:
- tourner à gauche (A) (I)
- tourner à droite (E) (P)
- tout droit (Z) (O)
- glissement gauche-droit (D) (M)
- glissement droite-gauche (Q) (K)
Les touches seront respectivement AEZDQ et IPOMK pour le joueur 1 et 2.
1.5 Modularité et protection des données
Une attention particulière doit être accordée à ce point. Le projet devra être subdivisé en modules : avion, graphique, trajectoires, dégâts et duel, ce dernier comprenant le programme principal. Graphique comprendra la plus grande partie de l'interface graphique et l'affichage des éléments (terrain, avions, etc). Cela sous-entend que les modules avion, trajectoires et dégâts ne doivent comporter aucune fonction graphique directe.
Dans chaque module, il faut distinguer les fonctions et les variables qui leur sont propres. Pour cela, on préfixera leur nom d'un underscore (_), ce qui signifie dans la philosophie ouverte du langage que l'on ne souhaite pas qu'elles soient visibles (et donc directement utilisables) dans les autres modules. Cette “protection” est mise en œuvre si l'on effectue une importation au niveau de l'espace des noms global car, dans ces conditions, toute variable ou toute fonction préfixée d'un ”_” ne sera pas importée. Exemple :
# module1 _x = 0 def _f(): pass def g(): pass # module principal ou interpreteur python3 >>> from module1 import * >>> _x Traceback ( most recent call last ): File " < stdin > " , line 1 , in <module > NameError : name ' _x ' is not defined >>> _f () Traceback ( most recent call last ): File " < stdin > " , line 1 , in <module > NameError : name ' _f ' is not defined >>> g () >>>
1.6 Tests unitaires
Chaque module doit comporter des tests unitaires vérifiant la justesse de l'ensemble des fonctionnalités du module.
Un moyen simple est l'écriture de tests dans la partie conditionnelle d'exécution directe, par exemple :
def _f(): pass def g(): pass if __name__ == '__main__': _f() # test de la fonction _f() g() # test de la fonction g()
Une autre solution est la définition de fonctions spéciales dédiées aux tests (voire scénario de tests), utilisables avec l'application nosetests. Il est également possible d'intégrer ces tests dans ce qui s'appelle des doctests, c'est-à-dire intégrer un test et le résultat attendu dans le docstring de la fonction.
1.7 Options de réalisation
Différentes options au choix peuvent compléter le projet.
- animation des tirs (explosion, trace visuelle),
- introduction aléatoire de dégâts avec handicaps sur plusieurs tours (palonnier bloqué, etc),
- dégâts croissant d'entiers (avec une probabilité de plus en plus faible), sans dépasser 5 points par tir.
- nouvelles trajectoires.
1.8 CNG - exemples
Voici un petit exemple illustrant les instructions à effectuer pour ouvrir une fenêtre et tracer une ligne si clique gauche et tracer un cercle si clique droit.
import cng # fonction qui trace une ligne horizontale a l'appui d'une touche selon la # position du dernier clic de souris def trace_ligne(): cng.line(0, cng.get_mouse_y(), 300, cng.get_mouse_y()) # fonction qui trace une ligne horizontale a l'appui d'une touche selon la # position du dernier clic de souris def trace_cercle(): cng.circle(cng.get_mouse_x(), cng.get_mouse_y(), 30) # ouverture d'une fenetre de 300 sur 200 cng.init_window("essai", 300, 200) # associer une fonction a l'appui de la touche 'd ' cng.assoc_key('d ', trace_ligne) # associer une fonction a l'appui du bouton 1 de la souris cng.assoc_button(1, trace_cercle) cng.main_loop()
Exemple d'affichage et de rotation d'une image.
import cng # ouverture d'une fenetre de 300 sur 200 cng.init_window("essai", 300, 200) # chargement d'une image img = cng.image('fokker.png') # affichage de l'image dans la fenetre a la position (50 ,50) imgid = cng.image_draw(50, 50, img) # affichage de l'image apres rotation de 45 degres imgid = cng.image_rotate(img, imgid, 45) cng.main_loop()
2 Travail à réaliser en bref
Au minimum, votre projet contenir certaines fonctionnalités et paradigmes de programmation fondamentaux. Pour être un peu plus qu'un débutant:
- définir au moins les 5 modules (fichier .py)
- avion
- trajectoires
- graphique
- degats
- duel
- contenir des commentaires et docstrings
- implanter au minimum les 3 trajectoires suivantes: tout droit, virage gauche, virage droit
- définir complètement au moins un modèle d'avion
- simuler le déplacement et l'exécution des manœuvres sélectionnées
- gérer les points de structure
- gérer les tirs sur 360 degrés
- gérer les tours et la fin de partie
Pour commencer à être respectable
- présenter une interface graphique permettant de définir 3 manœuvres successives (les touches AZEQD et IOPKM)
- implanter au minimum les 5 trajectoires suivantes: tout droit, virage gauche, virage droit, glissement gauche-droit, glissement droit-gauche
- se lancer en ligne de commande avec le nom des deux avions en argument
- gérer les tirs selon un angle de tir limité
- définir au moins 4 modèles d'avions différents
- (undisclosed)
Pour qu'on vous regarde d'un bon œil
- intégrer les options proposées
- intégrer des options non proposées intéressantes
3 Travailler à la maison
Pour travailler chez vous avec l'interface graphique:
Version compliquée mais qui sera comme à l'université (explication pour Linux):
Il faut installer:
- Python-3.2.3 (disponible dans toutes les distributions sous formes de paquet)
- Pillow (version compatible python3 de PIL pour la manipulation
d'images)
- Récupérer les sources de Pillow
- Décomprésser les sources: ``tar xzvf Pillow-2.3.1.tar.gz`` (ou plus)
- Compiler les sources:
- ``cd Pillow-2.3.1/``
- ``python3 setup.py build``
- Vérifier qu'il n'y a pas eu de problème et qu'il y a bien la prise en charge de Tkinter, la Zlib et des images JPEG
- Installer en tant qu'administrateur
- ``sudo python3 setup.py install`` (Ubuntu/Debian)
- ou bien : ``su`` puis ``python3 setup.py install`` (Fedora)
- Eventuellement tester l'installation et la compilation
- ``python3 selftest.py``
- Installer la librairie cng
- Récupérer le fichier ``/usr/lib/python3.2/cng.pyc`` depuis une des machines de l'université (ou la page du projet)
- Placer ce fichier dans votre répertoire de travail (avec les fichier du projet)
Version simple, passer en python2: Dans ce cas il faut juste
- Installer python-2.7.3
- Installer la librairie cng
- Récupérer le fichier ``/usr/lib/python2.7/cng.pyc`` depuis une des machines de l'université (ou la page du projet)
- Placer ce fichier dans votre répertoire de travail (avec les fichier du projet)
Attention aux problèmes d'incompatibilités qui pourraient apparaitrent en passant de votre version 2.7.3 à 3.2.3 (principalement la commande ``print``)